物理学上的直线,跟你的想象不一样
作者:佚名 人气:
次 时间:2019年08月23日 星级:

这是一个很有意思的话题,本文将竭尽所能与各位小伙伴探讨一下直线的概念。
欧氏几何钟的图形
一、数学上的直线定义
我们在中学开始接触几何和数学的时候,直线就可以有几何定义和数学的定义。在平面几何上,直线是点在空间内沿相同或相反方向运动的轨迹。或者定义为:曲率最小的曲线(以无限长为半径的圆弧)。
从平面解析几何的角度来看,平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形,即y=kx+b,k被称为该直线的斜率,b是当x=0时,y的值。
在三维空间中,两个平面相交的交线为一条直线。因此,在三维空间直角坐标系中,用两个表示平面的三元一次方程联立,作为它们相交所得直线的方程。
空间直线的方向用一个与该直线平行的非零向量来表示,该向量称为这条直线的一个方向向量。直线在空间中的位置, 由它经过的空间一点及它的一个方向向量完全确定。
在非欧几何中直线指连接两点间最短的线,又称短程线。方向向量:截取直线l上两点A(l,n,0)和B(k+l,m+n,1)方向向量为:AB=(k,m,1)

平面直角坐标系中的直线
二、对欧氏几何中直线定义的质疑
我们从前面的定义中可以看到,在欧几里得几何学中,点、直线、平面都是直观的几何对象。在建立欧几里得几何学的公理体系时,直线与点、平面等都是不加定义的,我们把它们当作“真理”,它们之间的关系则由所给公理刻画。
现在我要质疑欧氏几何的哪方面呢?我当然不可能去质疑,过两点有且仅有一条直线。我只想质疑它的真实性问题。因为对于几何来说,它的基本概念跟我们理解的真实物体之间是没有什么关系的,都是抽象的概念。
然而几何中的这些点、线、面其实都是跟我们经验世界中的物体相对应的。毫无疑问,这些经验中的客观存在的物体,是我们几何中的点、线、面的概念的由来。从这个角度去说的话,其实我们可以把欧式几何中的点、线、面,与物理学上的刚体(或者是我们认为不会变形的物体)上的点、线、面相对应。这样一来,几何中的点、线、面都可以看作是物体上的点、线、面。这样我们就可以去讨论这些基本概念的真实性问题了。

几何物体上的直线
三、物理学上的“直线”概念
在这里我要提一下物理学中的最小作用量原理。在生活中我们可以发现很多的极值现象,比如水总是往低处流、一根两端悬挂起来的线会自然弯成一道弧线,太空中的星体和水滴都不约而同地选择球体这个形状。骨头、羽毛、植物的茎、蜂巢、蚂蚁窝的构造,都是最符合自身的目的,又是最节省原材料的。这些自然现象的背后,就是最小作用量原理。
那么这个最小作用量原理跟直线有什么关系吗?
可以说关系很大。我们在前面定义直线的时候就有一个基本的公理:两点间线段最短。可以说直线就是这样一条线,它上面的任意两点间的最短距离都在这条线上。从这个角度来说,要考察一条线是不是直线,我们需要考核这条线上的两个点之间的最短距离在不在这条线上。很显然,我们如果从这个角度去考核什么是直线,就必须考虑这个几何问题的物理实在性问题。
如今,广义相对论已经被大量的观测事实所证明,观测事实告诉我们,光线在大质量天体附近沿着“最短路径”即测地线方向前进。所以我们看到,真正的“直线”并不是直线。这就是广义相对论告诉我们的时空弯曲。所以从物理学的角度来说,所谓的直线,是真空中光走过的路径。
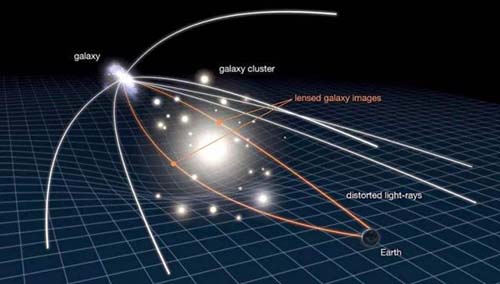
星光偏折现象
全文总结
我们从传统的欧式几何的直线概念,谈到了几何概念的物理意义,又从最小作用量原理给出了物理学上的直线概念。希望本文能对各位小伙伴对于直线这个概念有一个重新的认识。
- 上一份资料:理论物理学四大辉煌时期,最后一个,爱因斯坦一生都未曾解开
- 下一份资料:2019年诺贝尔物理学奖揭晓 3位科学家获奖

这是一个很有意思的话题,本文将竭尽所能与各位小伙伴探讨一下直线的概念。

欧氏几何钟的图形
一、数学上的直线定义
我们在中学开始接触几何和数学的时候,直线就可以有几何定义和数学的定义。在平面几何上,直线是点在空间内沿相同或相反方向运动的轨迹。或者定义为:曲率最小的曲线(以无限长为半径的圆弧)。
从平面解析几何的角度来看,平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形,即y=kx+b,k被称为该直线的斜率,b是当x=0时,y的值。
在三维空间中,两个平面相交的交线为一条直线。因此,在三维空间直角坐标系中,用两个表示平面的三元一次方程联立,作为它们相交所得直线的方程。
空间直线的方向用一个与该直线平行的非零向量来表示,该向量称为这条直线的一个方向向量。直线在空间中的位置, 由它经过的空间一点及它的一个方向向量完全确定。
在非欧几何中直线指连接两点间最短的线,又称短程线。方向向量:截取直线l上两点A(l,n,0)和B(k+l,m+n,1)方向向量为:AB=(k,m,1)

平面直角坐标系中的直线
二、对欧氏几何中直线定义的质疑
我们从前面的定义中可以看到,在欧几里得几何学中,点、直线、平面都是直观的几何对象。在建立欧几里得几何学的公理体系时,直线与点、平面等都是不加定义的,我们把它们当作“真理”,它们之间的关系则由所给公理刻画。
现在我要质疑欧氏几何的哪方面呢?我当然不可能去质疑,过两点有且仅有一条直线。我只想质疑它的真实性问题。因为对于几何来说,它的基本概念跟我们理解的真实物体之间是没有什么关系的,都是抽象的概念。
然而几何中的这些点、线、面其实都是跟我们经验世界中的物体相对应的。毫无疑问,这些经验中的客观存在的物体,是我们几何中的点、线、面的概念的由来。从这个角度去说的话,其实我们可以把欧式几何中的点、线、面,与物理学上的刚体(或者是我们认为不会变形的物体)上的点、线、面相对应。这样一来,几何中的点、线、面都可以看作是物体上的点、线、面。这样我们就可以去讨论这些基本概念的真实性问题了。

几何物体上的直线
三、物理学上的“直线”概念
在这里我要提一下物理学中的最小作用量原理。在生活中我们可以发现很多的极值现象,比如水总是往低处流、一根两端悬挂起来的线会自然弯成一道弧线,太空中的星体和水滴都不约而同地选择球体这个形状。骨头、羽毛、植物的茎、蜂巢、蚂蚁窝的构造,都是最符合自身的目的,又是最节省原材料的。这些自然现象的背后,就是最小作用量原理。
那么这个最小作用量原理跟直线有什么关系吗?
可以说关系很大。我们在前面定义直线的时候就有一个基本的公理:两点间线段最短。可以说直线就是这样一条线,它上面的任意两点间的最短距离都在这条线上。从这个角度来说,要考察一条线是不是直线,我们需要考核这条线上的两个点之间的最短距离在不在这条线上。很显然,我们如果从这个角度去考核什么是直线,就必须考虑这个几何问题的物理实在性问题。
如今,广义相对论已经被大量的观测事实所证明,观测事实告诉我们,光线在大质量天体附近沿着“最短路径”即测地线方向前进。所以我们看到,真正的“直线”并不是直线。这就是广义相对论告诉我们的时空弯曲。所以从物理学的角度来说,所谓的直线,是真空中光走过的路径。

星光偏折现象
全文总结
我们从传统的欧式几何的直线概念,谈到了几何概念的物理意义,又从最小作用量原理给出了物理学上的直线概念。希望本文能对各位小伙伴对于直线这个概念有一个重新的认识。
- 上一份资料:理论物理学四大辉煌时期,最后一个,爱因斯坦一生都未曾解开
- 下一份资料:2019年诺贝尔物理学奖揭晓 3位科学家获奖


 会员登录
会员登录
用户评论
(以下评论仅代表网友意见,与本站立场无关)